ミニ四駆ジャパンカップ2014開幕:フジヤマチェンジャーを物理する #mini4wd
2014.06.23ナイアガラ・スロープに引き続き、今年の難関「フジヤマチェンジャー」の角度、クリア可能な速度を物理計算にて求めます。
ミニ四駆ジャパンカップ2012参加レポート(3):ナイアガラ・スロープを物理する #mini4wd【ワンダードライビング】
※これは独自調査・考察です。ここでの数値はあくまでも推定値に基づく計算値であり、実際とは異なることがありますので予めご了承ください。
射出角度を求める
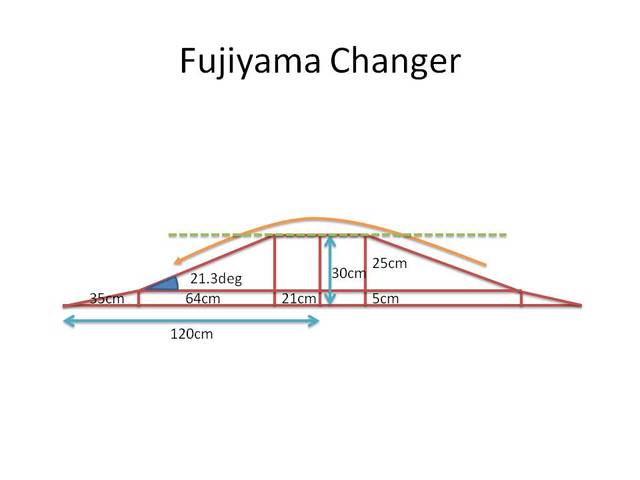
まず写真をもとに、フジヤマチェンジャーのスロープの高さ、各部の長さを求めます。
射出角度を求める
次に三角関数を使い、射出角度を求めます。
θ = atan( 25 / 64 ) = 0.3724 [rad] (21.33度)
21度と求められました。
着地位置について
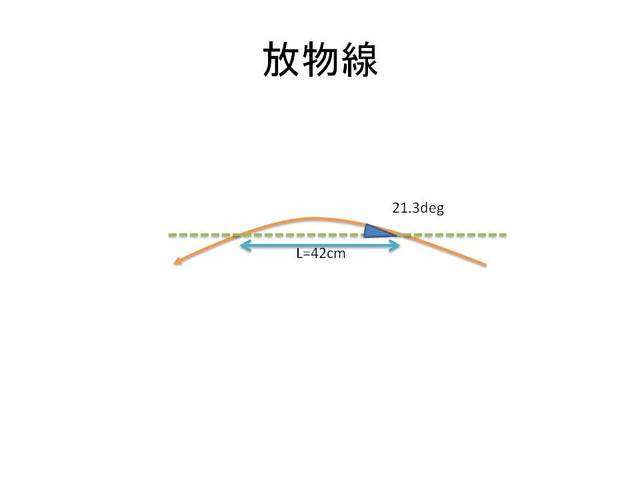
射出角度で投射し、着地する場所はスロープ上でなければなりません。今回はナイアガラスロープと異なり、スロープがひねっているためにスロープ後端ではなく水平部分からスロープになる位置、つまり21cm x 2つ = 42cmの場所を狙う必要があります。
放物運動計算から初速を求める
初速を v0 (ブイゼロ)とすると、それぞれのx, y成分は
v0x = v0 cos θ
v0y = v0 sin θ
飛んでいる時間を tとすると
飛距離L = v0x * t
鉛直方向(y方向)の速度 vyは重力が作用し、いずれ0となり、今度は逆に重力加速度で加速します。
頂点に達したときvy = 0となりますが、そのときのtを求めます。
vy = v0y - gt = 0
t = v0y / g
放物運動なので、再び基準点に戻る時間は二倍の 2tとなります。この時のx成分が飛距離Lとなり、Lは
L = v0x * (2t) = v0 cos θ x 2 * (v0y / g )
= ( 2 v0 ^2 * cos θ * sin θ ) / g
v0を求めたいので式を変形します。
v0^2 = ( g * L ) / ( 2 * cos θ * sin θ )
公式 2 cos θ sin θ = sin 2θ を使い、さらに変形、平方根を求めます。
v0 = sqrt ( ( g * L ) / ( sin 2 * θ ))
ここで、数値を代入します。
L = 0.42 [ m ]
g = 9.8 [m/s]
θ = atan ( 25 / 64 ) [rad]
v0 = sqrt( 9.8 * 0.42 / sin (2*atan(25/64)))
= 2.46 [m/s]
≒ 2.5 [m/s ]
この計算では着地を42cm先としていますが、スロープには壁があるので壁にぶつけることを考えると、実際には50cm前後でも越えることは可能と思われます。
実測から速度を計算
ミニ四駆ジャパンカップ2014開幕:レース動画特集 #mini4wd【ワンダードライビング】
オープンクラス優勝マシンがフジヤマチェンジャーのスロープ部、1.2mを経過するのに所要した時間 0.478秒。
ここから速度を逆算してみます。
v = 1.2[m] / 0.478 [s]
= 2.510 [m/s]
よって理論値と実測がほぼ同等だったことが分かります。